从零开始编写感知机

摘要：本文使用python numpy完成简单感知机的搭建，并对sklearn iris鸢尾花数据集进行线性二分类。

感知机的原始形式利用线性函数 \(y = w \cdot x + b\) 和二值化函数 \(y = sign(x) = x \gt 0\ ?\ 1 : -1\)，实现对数据的二分类，优化参数采用梯度下降的方法，即随机选取误分类点 \((x_0,y_0)\) (判断误分类点方法 \(y_i * (w \cdot x_i + b) \le 0\) )，优化参数 \(w=w+n*y_0*x_0\)，\(b=b+\eta *y_0\) (\(\eta\) 为学习率)，直到没有误分类点便结束计算。

另外需要说明的是，感知机算法得以实现的前提是误分类次数 \(k\) 是有上限的，因此经过一定的迭代次数后必然能得到最终结果，误分类次数 \(k\) 满足不等式：

$$k \le (\frac{R}{\gamma})^2$$

1.导入所需库

import numpy as np
import matplotlib.pyplot as plt   #绘制图表库
import random
from sklearn.datasets import load_iris   #导入数据集

2.数据集的导入与预处理

首先导入数据集，用load_iris函数导入sklearn内部数据集，data方法和target方法分别用于获取数据样本和对应标签集

iris = load_iris()
x = iris.data  #数据
y = iris.target #标签

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]

打印标签数据可知，数据集中共有三类标签数据，每类50条数据。由于感知机用于二分类，故仅选取前100条即可。这里为了简化计算，仅选取每条数据的前两个数据值（分别对应花萼的长度和宽度）进行分类。

#选取前两类数据
x = x[0:100,[0,1]]
y = y[0:100]
n_rate = 1     #学习率

将0/1标签数据改为-1/1，方便之后判断误分类点并利用梯度下降方法调整参数。

#将标签设置为1或-1
for i in range(y.shape[0]):
    if y[i] == 0:
        y[i] = -1

初始化参数 \(w,b\)，这里将参数都初始化为 \(0\)，且 \(w\) 的维度要与输入数据一致。

w,b = np.zeros(2),0   #初始化参数
epoche = 0            #记录迭代次数

接着就是训练过程，首先使用当前参数遍历整个数据集，找出所有误分类点，然后随机选取一个误分类点进行参数的优化，循环这个过程直到没有误分类点。

#开始训练
while True:
    epoche += 1
    mistake_count = 0
    mistake_list = []

    for i in range(y.shape[0]):        #遍历找出误分类点
        if y[i]*(w@x[i]+b) <= 0:
            mistake_count += 1
            mistake_list.append(i)

    if mistake_count == 0:              #判断是否存在误分类点
        break

    rand_i = random.choice(mistake_list)    #随机选择误分类点，优化参数
    w += n_rate*y[rand_i]*x[rand_i]
    b += n_rate*y[rand_i]

最后绘图将结果可视化。

print('迭代次数：',epoche)
print('w=',w,',b=',b)
x_plot = np.linspace(4,7,10)                       #根据数据特点建立x轴参数
y_plot = -(w[0]*x_plot+b) / w[1]
plt.plot(x_plot,y_plot)                           #绘制分类直线
plt.plot(x[:50,0],x[:50,1],'rx',label='0')        #显示所有数据点
plt.plot(x[50:100,0],x[50:100,1],'bo',label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
plt.show()

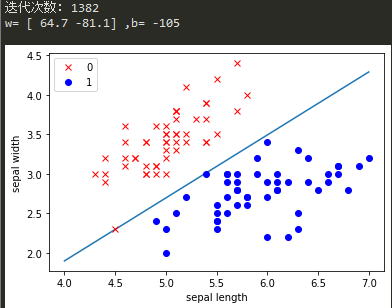
最终运行结果如下：