使用Python+OpenCV实现图像的基本运算处理
本文使用使用Python+OpenCV 实现数字图像的基本运算方法和基础的图像处理操作 ,包括:图像的读取、显示、存储;图像的基本运算(图像代数运算、几何运算以及直方图均衡化);补充概念介绍(CCD、CMOS、白平衡)。
1. 图像的读取、显示、存储
首先从网上下载了12张灰度图片,用于本次实验,图片集如下 。
👉点击这里下载数据集
图像的读取:在Python中使用cv2模块的imread()函数读取图像,读取时需要设置以灰度图像模式读取,否则默认为三通道彩色。读取的图像为numpy数组,可以很方便的对数组对象做进一步操作。
图像的显示:图像读取完成后进行相应的显示,使用imshow()函数显示图像,函数需要指定图像窗口名称和图像路径。实验中我一次性读取了7张图像并显示,显示完成后等待任意键盘按键关闭所有窗口。
相关代码如下:
import cv2
import numpy as np
for i in range(7):
img = cv2.imread('imageSet/'+str(i+1)+'.png',cv2.IMREAD_GRAYSCALE) #以灰度模式读取图像
cv2.imshow(str(i+1), img) #显示图像
cv2.waitKey(0) #等待任意键盘按键
cv2.destroyAllWindows() #关闭图像窗口
读取的结果如下 :
图像的保存:使用imwrite()函数将一个numpy数组保存为指定格式的图像。我手动创建了三个50×50的numpy数组,分别代表rgb三种颜色,使用merge()函数将它合并后保存。
r = np.array([[203 for i in range(50)] for j in range(50)]).astype(int)
g = np.array([[90 for i in range(50)] for j in range(50)]).astype(int)
b = np.array([[24 for i in range(50)] for j in range(50)]).astype(int)
img = cv2.merge([r,g,b]) #合并一张50x50的纯色RGB图像
cv2.imwrite('save.png', img) #图像的保存
打开保存的图像查看:
是一个50×50的蓝色方块 。
2. 图像的基本运算(图像代数运算、几何运算以及直方图均衡化)
2.1 图像的代数运算
2.1.1 加法运算——去除叠加性噪声
图像的加法运算可以去除图像的叠加性噪声,当对多张图像含有同一随机噪声的图像相加并取平均值后,由于噪声完全随机,所以均值为0,可以显著降低噪声对图像的影响。
实验中我首先读取了一张图片,然后通过随机取点的方式为图片添加噪声数据,并重复生成若干张噪声图像。最后通过numpy数组加法运算对这些图像做均值操作,显示处理后的结果。
import cv2
import numpy as np
img = cv2.imread('imageSet/8.png', cv2.IMREAD_GRAYSCALE) #读取一张图像
addNum = 32 #叠加数量
def noiseGenerator(img): #噪声生成器
img = img.copy()
n = int(img.shape[0] * img.shape[1] * 0.02)
ilist = np.random.randint(0, img.shape[1], n)
jlist = np.random.randint(0, img.shape[0], n)
for k in range(n):
i = ilist[k]
j = jlist[k]
img[j, i] = 255
return img
imgsWithNoise = []
for i in range(addNum):
imgsWithNoise.append(noiseGenerator(img)) #给原图加噪声
res = np.zeros((img.shape[0], img.shape[1]))
for i in range(addNum):
res += imgsWithNoise[i]
res /= addNum #均值去噪
res = res.astype('uint8')
cv2.imshow('res', res)
cv2.waitKey(0)
cv2.destroyAllWindows()
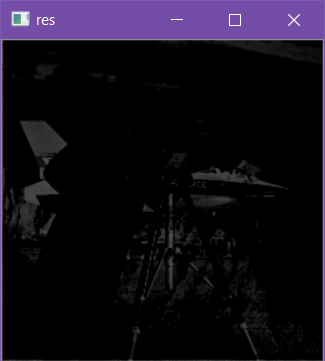
下面分别是叠加数量为1,4,8,32时的处理结果。

可以看到,当叠加数量达到32时已经基本消除了噪声对图像的影响。
2.1.2 加法运算——图像的叠加
使用addWeighted()函数可以将两张图像按照特定的比例做加法运算从而实现图像的叠加效果。
这里我按照0.5的比例将两图像叠加到一起。
import cv2
import numpy as np
img1 = cv2.imread('imageSet/1.png', cv2.IMREAD_GRAYSCALE)
img2 = cv2.imread('imageSet/6.png', cv2.IMREAD_GRAYSCALE)
img = cv2.addWeighted(img1, 0.5, img2, 0.5, 0)
cv2.imshow('res', img)
cv2.waitKey(0)
cv2.destroyAllWindows()
叠加产生的效果如下,看上去像两张半透明的图像合成在一起。

2.1.3 减法运算——混合图像的分离
将上面产生的混合图像重新分离,只需在上面代码的基础上多加入一步减法运算即可,注意在相减之前先将原图像像素值加倍来还原原始效果。
splitImg = img * 2 - img2

生成的结果又显示出了混合之前的图像1 。
如果不加倍直接使用减法函数相减的话则会出现大量0值,失去原始图像真实性。
splitImg = cv2.subtract(img, img2)
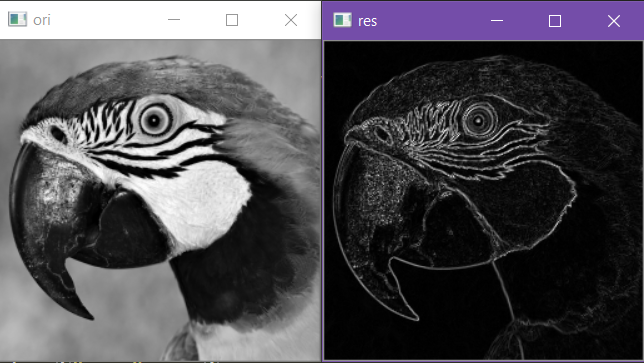
2.1.3 减法运算——图像差分提取边缘
对图像做减法的差分运算可以简单的提取出图像边缘,具体的,分别在水平方向和垂直方向做差分运算(即在对应方向上使用平移一个像素后的图像与原图像做减法),接着将两个方向上得到的边缘信息结果相加便可以得到整幅图像的边缘信息。相加的时候进行归一化处理避免像素值超限。
import cv2
import numpy as np
img = cv2.imread("imageSet/7.png", cv2.IMREAD_GRAYSCALE)
#水平一阶差分
X = np.fabs(img[:, :-1].astype('int8') - img[:, 1:].astype('int8'))[:-1].astype('uint8')
#垂直一阶差分
Y = np.fabs(img[:-1].astype('int8') - img[1:].astype('int8'))[:,:-1].astype('uint8')
res = X + Y
#归一化
res = (((res - np.min(res)) / np.ptp(res)) * 255).astype('uint8')
cv2.imshow("ori",img)
cv2.imshow("res",res)
cv2.waitKey(0)
cv2.destroyAllWindows()
2.2 图像的几何运算
2.2.1 图像的平移
图像平移需要平移的变换矩阵,以齐次坐标的形式表示,图像向右平移100像素,向下平移50像素的变换矩阵为[[1, 0, 100], [0, 1, 50]]。
使用warpAffine()函数对一幅图形进行指定变换矩阵的变换,传入参数分别表示源图像,变换矩阵和输出图像的大小,变换后显示结果。
import cv2
import numpy as np
img = cv2.imread('imageSet/10.png', cv2.IMREAD_GRAYSCALE)
move = np.array([[1, 0, 100], [0, 1, 50]]).astype('float32')
rows, cols = img.shape
img2 = cv2.warpAffine(img, move, (cols, rows))
cv2.imshow('res', img2)
cv2.waitKey(0)
cv2.destroyAllWindows()

2.2.2 图像的旋转
类似于图像的平移,图像旋转也需要先生成图像的旋转矩阵,函数getRotationMatrix2D()可以帮助生成该矩阵,其中所需的参数分别为旋转中心,旋转角度和缩放比例。
我希望以图像中心作为旋转中心,逆时针旋转15度,保留原图大小,因此填入参数:
move = cv2.getRotationMatrix2D((cols // 2, rows // 2), 15, 1)
有了变换矩阵后依然使用warpAffine()函数进行变换,但旋转还需要考虑插值的问题,因为图像旋转后由于像素点都是整数值,因此必然会产生很多的空洞点,需要插值处理。这里我分别采用双线性插值和最近邻插值的方法进行旋转变换,其中线性插值也是该函数的默认值。
import cv2
import numpy as np
img = cv2.imread('imageSet/10.png', cv2.IMREAD_GRAYSCALE)
rows, cols = img.shape
move = cv2.getRotationMatrix2D((cols // 2, rows // 2), 15, 1)
res = cv2.warpAffine(img, move, (cols, rows), flags=cv2.INTER_LINEAR)
res2 = cv2.warpAffine(img, move, (cols, rows), flags=cv2.INTER_NEAREST)
cv2.imshow('res', res)
cv2.imshow('res2', res2)
cv2.waitKey(0)
cv2.destroyAllWindows()
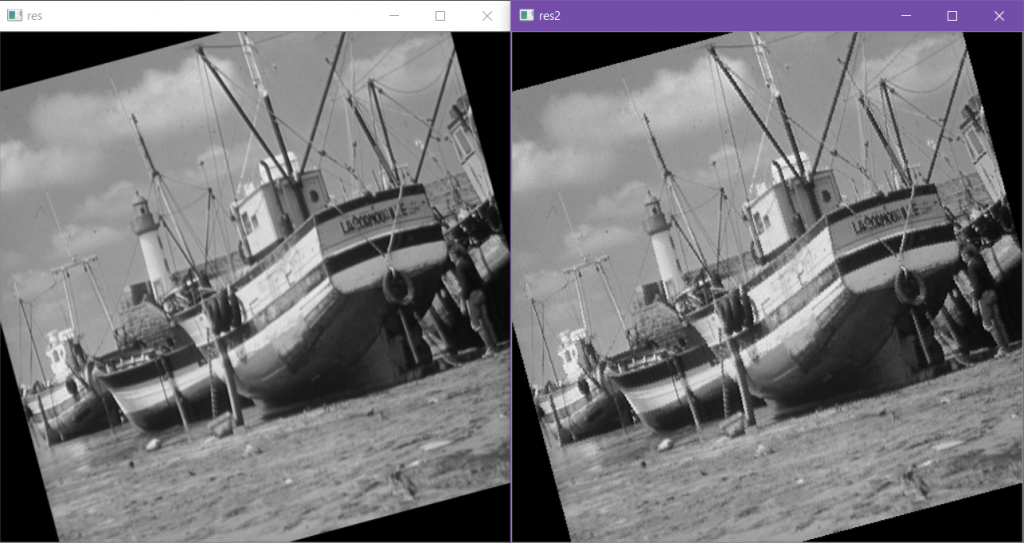
结果显示的两幅图像,分别采用了上述两种插值方法 。
2.2.3 图像的缩放
图像缩放采用resize()函数,函数内可以指定具体的输出的缩放后图像大小,也可以传入x和y方向的缩放比例自动计算(此时需指定输出大小为(0,0))。类似于旋转,缩放也需要进行插值处理。我采用像素区域关系重采样的方法将图像缩小到原图的二分之一。
import cv2
import numpy as np
img = cv2.imread('imageSet/10.png', cv2.IMREAD_GRAYSCALE)
rows, cols = img.shape
res = cv2.resize(img, (cols//2, rows//2), interpolation=cv2.INTER_AREA)
cv2.imshow('res', res)
cv2.waitKey(0)
cv2.destroyAllWindows()
结果如下:

2.3 图像的直方图均衡化
直方图的绘制:
绘制图像的直方图需要用到绘图库matplotlib。
使用cv2.calcHist()函数获取图像的直方图绘制数据,该函数需要传入参数[图像],[通道(灰度图像为0)],计算区域(整幅图为None),[像素区段数目],[像素取值范围]。
获得hist后使用plt.plot(hist)函数绘制直方图,plt.show()显示直方图。
首先来显示一幅图像的原始直方图。
import cv2
from matplotlib import pyplot as plt
img = cv2.imread('imageSet/10.png', cv2.IMREAD_GRAYSCALE)
#原图像
cv2.imshow('img', img)
hist = cv2.calcHist([img], [0], None, [256], [0, 256])
plt.plot(hist)
plt.show()
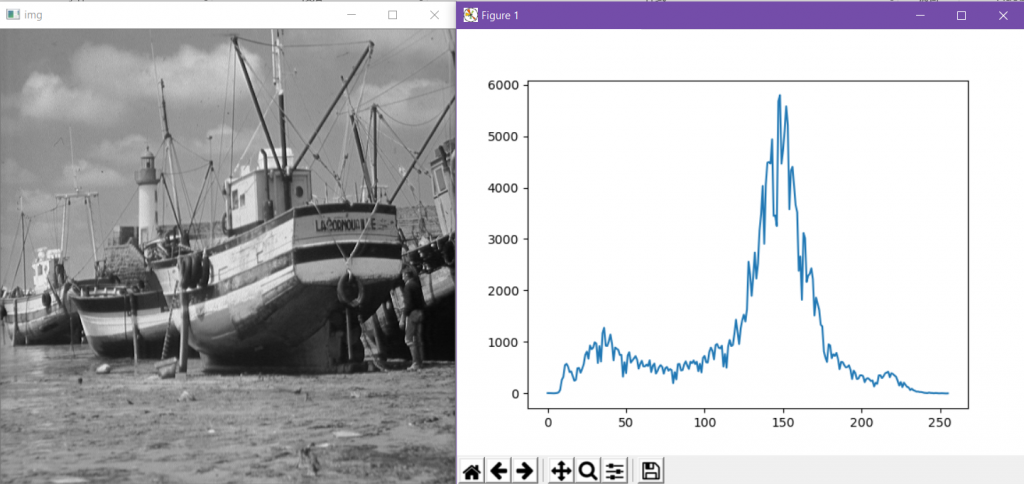
可见这幅图像的直方图分布还是十分均匀的,为了达到直方图均衡化的效果,我先使用线性运算的方法降低了图像的亮度和对比度,使像素值分布到0~50的区间之中,从而形成一张直方图分布偏左的图像。
#对比度低亮度低的图像
img = (img / 255 * 50).astype("uint8")
cv2.imshow('img', img)
hist = cv2.calcHist([img], [0], None, [256], [0, 256])
plt.plot(hist)
plt.show()
形成的图像和直方图:
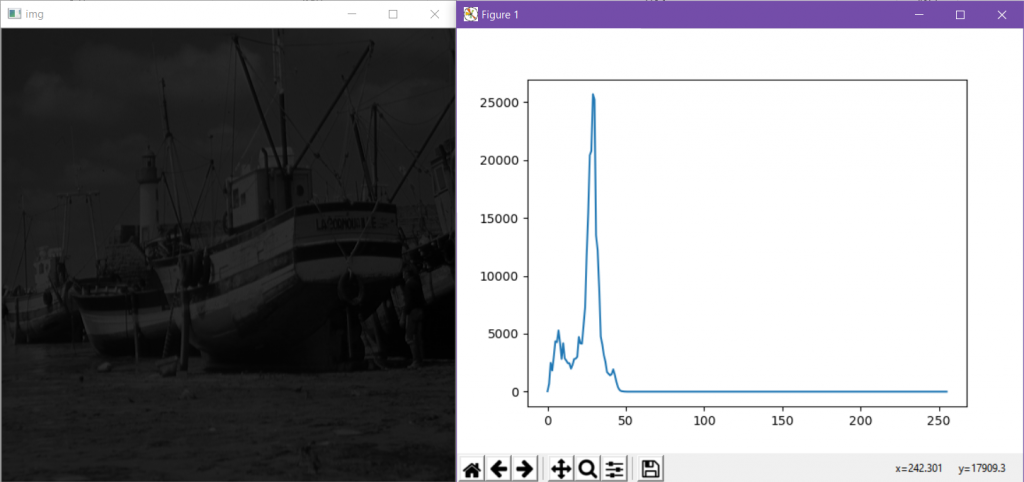
这幅图像明显色调偏暗且细节展示不清晰,而它的直方图分布在左侧。
下面使用cv2.equalizeHist()函数来均衡化直方图。
#直方图均衡化后的图像
img = cv2.equalizeHist(img)
cv2.imshow('img', img)
hist = cv2.calcHist([img], [0], None, [256], [0, 256])
plt.plot(hist)
plt.show()
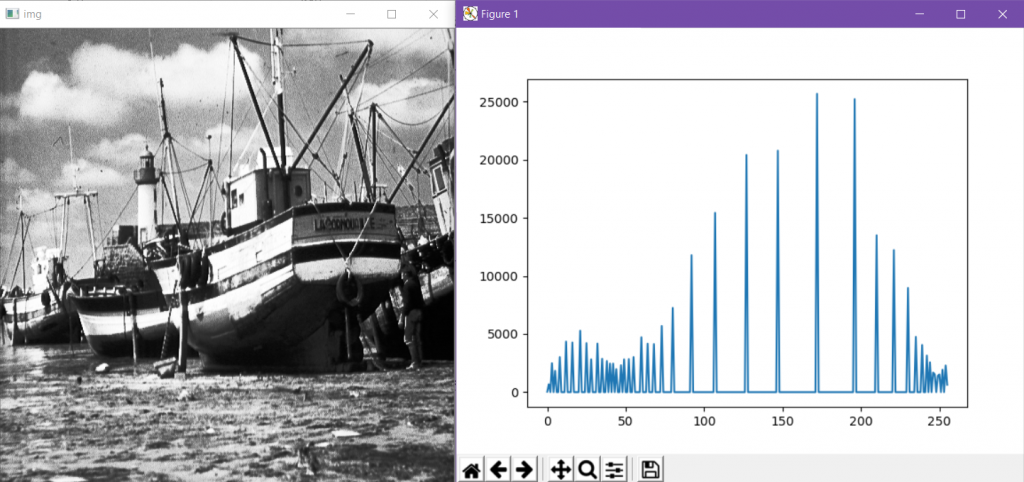
图像清晰了很多,虽然和原始图像比丢失了很多像素值,但是和上一幅图像相比明显将图像增亮增大了对比度,使整体和细节都清晰可见,而直方图也比较好的分布在了整个像素灰度区间之中。
我又通过手动计算模拟了一遍直方图均衡化的过程。
#手动直方图均衡化
img_shape = img.shape #保存图像的大小
img = img.ravel() #转换为一维数组
hist = {} #存储不同像素值出现的次数
for i in img:
hist[i] = hist.get(i, 0) + 1 #计算不同像素值出现的次数
for i in hist: #将次数除以总像素数,进行归一化,得出频率
hist[i] /= img.shape[0]
hist = sorted(list(hist.items())) #按照像素值从小到大排序
hist_equ = {} #存储均衡化后的对应像素值
sum_ = 0 #用于频率的累加
for i in hist:
sum_ += i[1] #累加频率
hist_equ[i[0]] = sum_ * 255 #扩展像素值
for i in range(img.shape[0]):
img[i] = hist_equ[img[i]] #根据对应像素值生成均衡化后的图像
img = img.astype('uint8').reshape(img_shape) #转换数据类型,恢复图像大小
cv2.imshow('img', img) #显示图像
hist = cv2.calcHist([img], [0], None, [256], [0, 256]) #生成直方图
plt.plot(hist)
plt.show() #显示直方图
具体的操作过程在对应代码处给出了详细的注释说明。
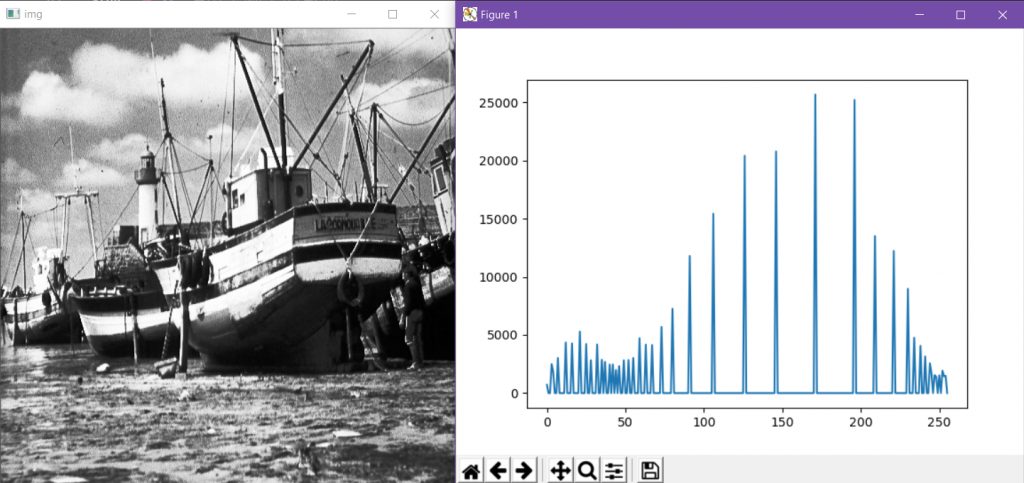
生成的结果与之前相同。
3. 补充内容
3.1 CCD和CMOS传感器
两种类型的传感器都以完全相同的方式检测光。入射光子撞击硅原子,硅原子是半导体。当发生这种情况时,原子中的一个电子被提升到更高的能级(轨道),称为导带。硅通常表现得像绝缘体,所以它的电子不能四处移动。但是一旦电子被提升到导带,就可以自由地移动到其他相邻的原子。在光学传感器中,这些现在可移动的电子被称为光电子。
两种类型的传感器都使用像素。像素只是硅的一个小方形区域,它收集并保持这些光电子。通常的比喻是田间的一系列水桶,每个都收集雨水。如果你想知道在该区域的任何部分下了多少雨,你只需要测量每个桶的充满程度。
电荷耦合器件(CCD)是更老,更成熟的技术。在读出期间,CCD 将电子从像素移动到像素,就像桶式旅一样。它们通过传感器一角的读出放大器一个接一个地移出。这样做的最大好处是每个像素都以相同的方式测量。使用单个读出放大器使读出过程非常一致。这样可以生成具有低固定模式噪声和读取噪声的高质量数据,像素中也没有浪费的空间。将所有光电子混洗到器件的一个角落确实限制了读出速度,这是 CMOS 传感器的问题。
大多数现代电子产品都是采用 CMOS 技术或互补金属氧化物半导体制造。使用 CMOS 技术构建传感器可以使用其他电子元件,例如模数转换器。CMOS 传感器中的每个像素都有自己的读出放大器,通常传感器每列都有 A / D 转换器,这使得可以非常快速地读出阵列。位于每个像素的晶体管占用一些空间,导致灵敏度较低。除了速度之外,开发 CMOS 传感器的主要动机是成本,而不是性能。多年来,CMOS 传感器的灵敏度,噪声和暗电流性能远远低于 CCD 传感器。
3.2 白平衡
白平衡基本概念是“不管在任何光源下,都能将白色物体还原为白色”,对在特定光源下拍摄时出现的偏色现象,通过加强对应的补色来进行补偿。相机的白平衡设定可以校准色温的偏差。
数码相机的白平衡设置是确保获得理想的画面色彩的重要保证。所谓的白平衡是通过对白色被摄物的颜色还原(产生纯白的色彩效果),进而达到其他物体色彩准确还原的一种数字图像色彩处理的计算方法。 摄像机内部有三个CCD电子耦合元件,他们分别感受蓝色、绿色、红色的光线,在预置情况下这三个感光电路电子放大比例是相同的,为1:1:1的关系,白平衡的调整就是根据被调校的景物改变了这种比例关系。比如被调校景物的蓝、绿、红色光的比例关系是2:1:1(蓝光比例多,色温偏高),那么白平衡调整后的比例关系为1:2:2,调整后的电路放大比例中明显蓝的比例减少,增加了绿和红的比例,这样被调校景物通过白平衡调整电路到所拍摄的影像,蓝、绿、红的比例才会相同。也就是说如果被调校的白色偏一点蓝,那么白平衡调整就改变正常的比例关系减弱蓝电路的放大,同时增加绿和红的比例,使所成影像依然为白色。