层次聚类算法之聚合聚类

层次聚类是一种无监督学习中的聚类方法，它将样本聚合到层次化的类中。层次聚类又可以分为聚合聚类（自下而上）和分裂聚类（自上而下）两种，本文主要讨论聚合聚类。

聚合聚类开始时将每个样本分到一个类，之后将相距最近的两类合并，重复此操作直到满足停止条件。

本文采用欧式距离来计算各个样本之间的距离，类间距离可以采用最短距离、最长距离和中心距离三种。

直接看代码。

导入所需库。

import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

导入数据集，数据集使用鸢尾花数据集的前一百条数据的中间两维特征。其中前50条数据属于一类，后50条属于一类，共两类。选用中间两维特征是由于这两个特征可以很清楚的区分两类数据。所以，我们的目标是把数据集分成两类。

dataSet = load_iris().data[:100,1:3]
#dataSet = np.delete(dataSet,41,axis=0)
size = dataSet.shape
categories_number = 2

为了避免数据的某个维度的值过大而主宰了样本间距离的计算结果，将数据进行归一化处理。

#归一化
mx = np.max(dataSet,axis=0)
mn = np.min(dataSet,axis=0)
dataSet = (dataSet - mn) / (mx - mn)

采用欧式距离计算两两样本之间的距离，提前保存所有的计算值。

#计算所有样本点间的欧氏距离（采用最小/最大/平均距离时使用）
distance = np.zeros((size[0],size[0]))
for i in range(size[0]):
    for j in range(size[0]):
        distance[i,j] = np.linalg.norm(dataSet[i] - dataSet[j])

根据聚合聚类自下而上的思想，使每个样本各自成为一类。

#将每个样本点（序号）加入到一个类中
categories = []
for i in range(size[0]):
    categories.append({i})

下面开始循环聚合的过程，首先判断终止条件：若剩余类别数等于所需分类的数，则停止。

while True:
    #若剩余类的数量满足条件，则退出循环
    if len(categories) == categories_number:
        break

计算类间距离，其中可以使用三种方法计算，分别是最短距离，最长距离和中心距离。

• 最短距离：两类中最近的两个样本之间的距离。
• 最长距离：两类中最远的两个样本之间的距离。
• 中心距离：两个类别的中心之间的距离。（所有样本点各个维度的均值即为类中心）

    #计算类间距离
    d_c = {}                                        #类间距离
    for c1 in range(len(categories) - 1):
        d_c[c1] = {}
        for c2 in range(c1 + 1, len(categories)):
            d_s = []                                #样本间距离
            def min_max_distance(flag):
                #最小(flag=False)或最大(flag=True)距离
                for s1 in categories[c1]:
                    for s2 in categories[c2]:
                        d_s.append(distance[s1,s2])
                d_s.sort(reverse=flag)
                d_c[c1][c2] = d_s[0]
            def centeral_distance():
                #中心距离
                center_c1 = np.zeros(size[1])
                for s1 in categories[c1]:
                    center_c1 += dataSet[s1]
                center_c1 /= len(categories[c1])
                center_c2 = np.zeros(size[1])
                for s2 in categories[c2]:
                    center_c2 += dataSet[s2]
                center_c2 /= len(categories[c2])
                d_c[c1][c2] = np.linalg.norm(center_c1 - center_c2)
            #min_max_distance(False)
            centeral_distance()

合并类间距离最小的两类。

    #排序找到最小的类间距离
    d_c_list = []
    for i in d_c.items():
        for j in i[1].items():
            d_c_list.append((i[0],)+j)
    d_c_list.sort(key=lambda a: a[-1])

    #合并类间距离最小的两个类
    nearest = [d_c_list[0][0],d_c_list[0][1]]
    categories[nearest[0]] = categories[nearest[0]].union(categories[nearest[1]])
    categories.pop(nearest[1])

循环结束后即可输出聚类的结果。

#输出结果
for i in range(len(categories)):
    print('第'+str(i+1)+'类：',categories[i])

为了更清晰的展示结果，绘制散点图。

#绘制散点图
for i in categories[0]:
    plt.plot(dataSet[i][0],dataSet[i][1],'rx')
for i in categories[1]:
    plt.plot(dataSet[i][0],dataSet[i][1],'bo')
plt.show()

分类结果如下：

第1类： {0，1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18，19，20，21，22，23，24，25，26，27，28，29，30，31，32，33，34，35，36，37，38，39，40，41，42，43，44，45，46，47，48，49}
第2类： {50，51，52，53，54，55，56，57，58，59，60，61, 62，63，64，65，66，67，68，69，70，71，72，73，74，75, 76，77，78，79，80，81，82，83，84，85，86，87，88，89, 90, 91, 92，93，94，95，96，97，98，99}

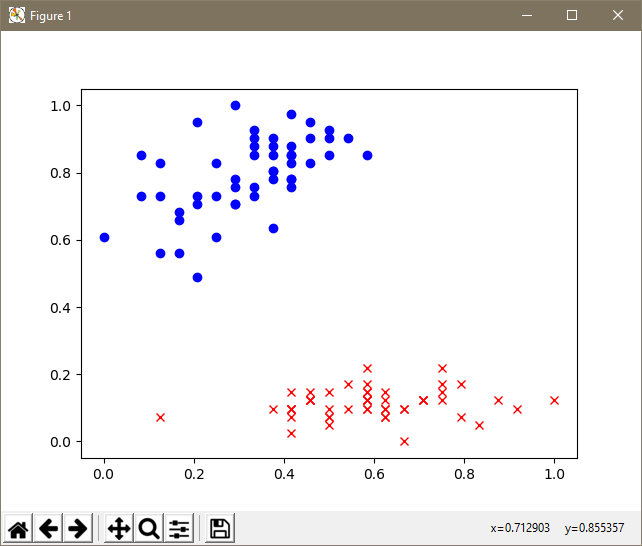
可见数据集被清楚的聚成了两类，聚类结果也是正确的。

当使用鸢尾花数据集的全部4个维度150条数据进行计算，此时结果因被分为3类。

由于4维数据难以清楚的图像化表示，因此只能取前两维绘图。

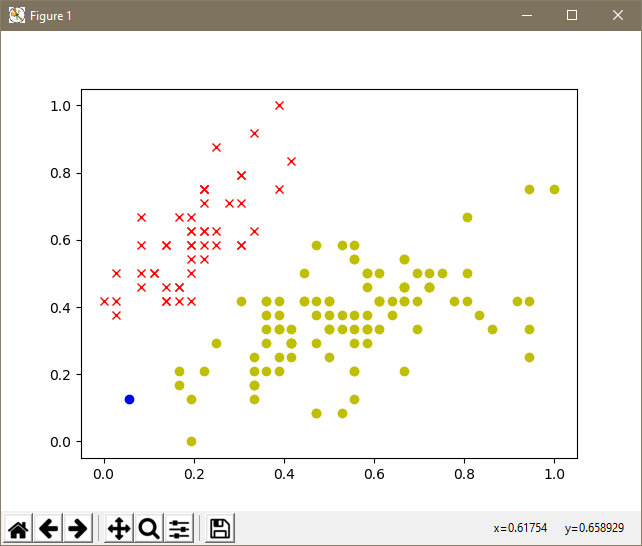
由于其中一个点可能是干扰数据或者噪音数据，其欧式距离较其他各个点更远，因此出现了某种极端的局部最优的结果，该点单独成为了一类，显然这与我们的期望是差别很大的。

聚合聚类对所有样本点间的距离都进行了细致的计算，并且聚类过程中不会进行整体的优化和二次计算，类别被不断地聚合扩充，导致很容易出现个别的噪声数据影响全局的情况发生。因此，对于距离区分不明显或含有噪音数据的数据集，聚合聚类很难很好的发挥作用，这是一大缺陷。